2022 03 29
1. 틀린 기록

2. 원인 분석
- 시간 초과 판정이 날 것이라고 생각은 했다. 왜냐하면 for문 두번에 모든 가능한 경우의 수를 구하고 dp 리스트에 저장하는 방식으로 풀었기 때문이다.
n = int(input())
dp = [[] for _ in range(n+1)] # 인덱스 1에 저장된 배열은 길이가 1인 계단의 수 모음
dp[1] = [1, 2, 3, 4, 5, 6, 7, 8, 9]
if n == 1:
print(9)
else:
for k in range(2, n+1):
for i in (dp[k-1]):
if i % 10 == 0:
str0 = str(i) + str(1)
dp[k].append(int(str0))
elif i % 10 == 9:
str9 = str(i) + str(8)
dp[k].append(int(str9))
else:
mok = i % 10
str1 = str(i) + str(mok-1)
str2 = str(i) + str(mok+1)
dp[k].append(int(str1))
dp[k].append(int(str2))
print(len(dp[n]) % 1000000000)- 이렇게 풀면 당연히 정답은 맞다. 하지만 시간 초과 판정을 받게 되므로, 모든 가능한 경우의 수를 구하는 것이 아니라, 가능한 숫자의 개수를 구하는 방법을 찾아야 했다.
3. 해결
import sys
input = sys.stdin.readline
n = int(input())
dp = [[0 for _ in range(10)] for _ in range(n)]
dp[0] = [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]
if n == 1:
print(sum(dp[n-1]))
else:
for i in range(1, n):
for j in range(0, 10):
if j == 0:
dp[i][j] = dp[i-1][j+1]
elif j == 9:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]
print(sum(dp[n-1]) % 1000000000)
- 동적 프로그래밍으로 풀어야 한다. 맨 뒤에 올 수 있는 숫자를 기준으로 개수를 세어서 배열에 저장하면 된다.
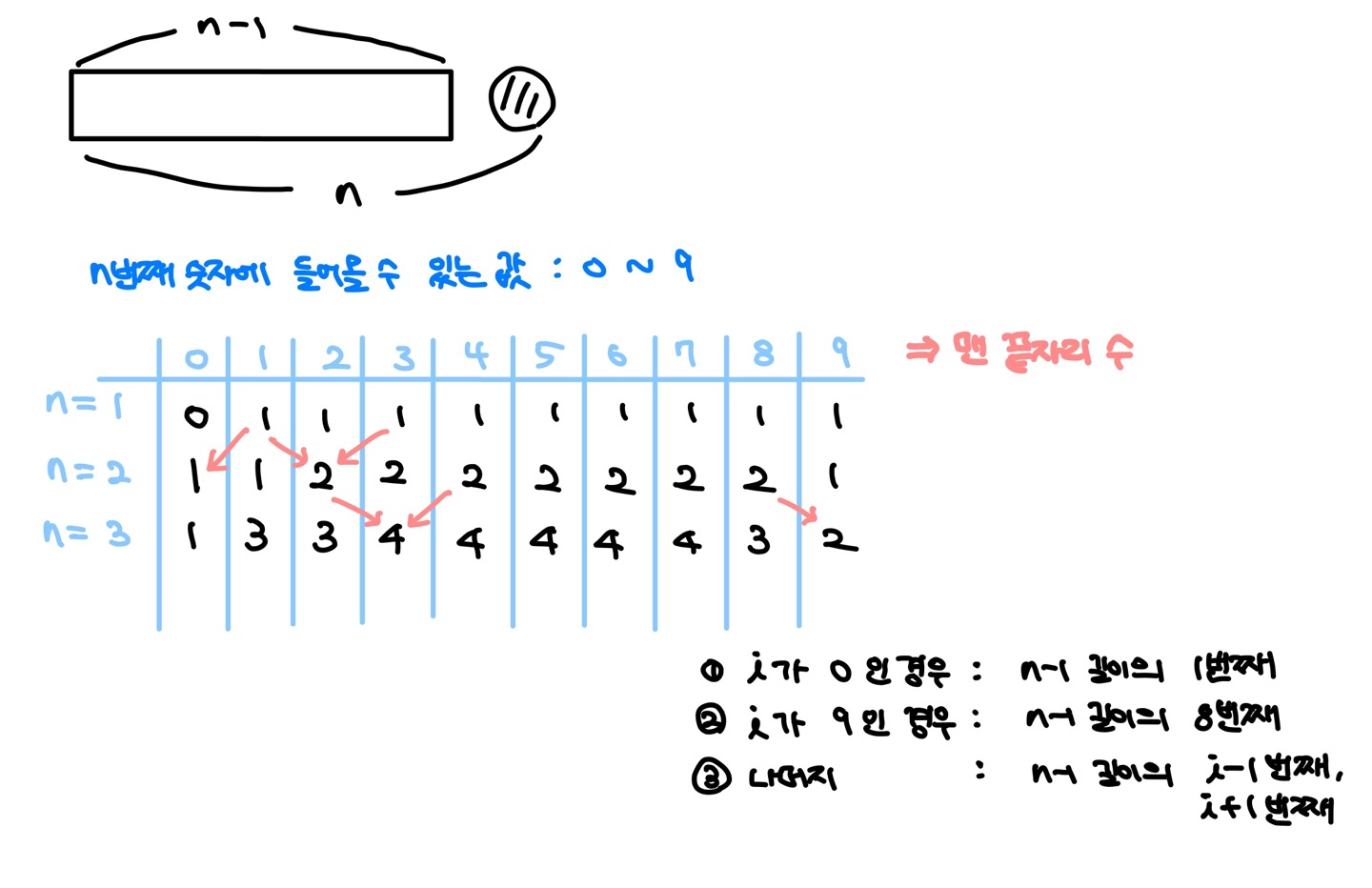
- 맨 끝자리에 특정 숫자 (0 ~ 9)가 왔을 때 만들어지는 계단 숫자의 개수를 정리해보면 위의 표와 같다.
1) 맨 끝자리 수가 0인 경우에는 그 전 숫자가 1일 수밖에 없다.
2) 맨 끝자리 수가 9인 경우에는 그 전 숫자가 8일 수밖에 없다.
3) 이외의 숫자는 (해당 숫자 - 1) 을 한 수 또는 (해당 숫자 + 1)을 한 수가 가능하다.
- 1)의 경우에는 dp[길이][맨 끝자리 수] = dp[길이 - 1][1]
- 2)의 경우에는 dp[길이][맨 끝자리 수] = dp[길이 - 1][8]
- 3)의 경우에는 dp[길이][맨 끝자리 수] = dp[길이 - 1][맨 끝자리 수 - 1] + dp[길이-1][맨 끝자리 수 + 1]
4. 배운 점
- 가능한 경우의 수를 표로 나타내보면서 규칙을 찾아야 한다.
- 웬만하면 직접 구하여 리스트에 저장하는 문제는 거의 없다. 개수를 물어본다면 규칙을 찾고 개수만을 구해야 한다.
'[ 알고리즘 ] > 오답노트' 카테고리의 다른 글
| [ BOJ 오답노트 ] 4179 C++ : 불! (0) | 2023.06.19 |
|---|---|
| [ BOJ 오답노트 ] 2156 파이썬 : 포도주 시식 (0) | 2022.03.30 |
| [ BOJ 오답노트 ] 2579 파이썬 : 계단 오르기 (0) | 2022.03.24 |
| [ BOJ 오답노트 ] 1149 파이썬 : RGB거리 (0) | 2022.03.22 |
| [ BOJ 오답노트 ] 1904 파이썬 : 01타일 (0) | 2022.03.12 |



